Information theory provides the tools to rigorously define the notion of security. A scenario that arises in certain cryptographic applications, such as quantum key distribution (QKD), involves two trustworthy parties (called Alice and Bob), along with an unwanted eavesdropper (called Eve). Each party has access to some (classical) system whose state is described by the random variable \(X\), \(Y\), and \(Z\), respectively. All these variables are correlated according to some joint probability distribution \(P_{XYZ}\). Alice and Bob’s goal is to utilize their shared correlations for private communication. Doing so involves processing their variables such that Eve’s overall correlation becomes decreased. Public communication between Alice and Bob can help in this task, and the operational framework is known as Local Operations and Public Communication (LOPC).
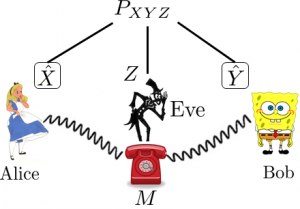
In an LOPC protocol, Alice and Bob attempt to transform their original variables \(X\) and \(Y\) into new variables \(\hat{X}\) and \(\hat{Y}\) such that
\(\begin{align} \text{(i)}& \qquad\hat{X}\approx\hat{Y}\\\text{(ii)}&\qquad I(\hat{X}:MZ)\approx 0, \end{align}\)
where \(M\) is the public communication generated in the protocol and \(I\) is the mutual information between \(\hat{X}\) and Eve’s variables. Intuitively, condition (i) says that \(\hat{X}\) represents shared randomness for Alice and Bob, while condition (ii) says that this randomness is almost completely uncorrelated from any information Eve might possess. In this case \(\hat{X}\) represents a secret key, or secrecy, that Alice and Bob share.
LOPC is a classical cryptographic analog of LOCC in the quantum setting. Whereas quantum entanglement is the fundamental resource in LOCC processing, classical secrecy is the fundamental resource in LOPC processing. Our research investigates the general theory of information-theoretic security in the LOPC setting, with the following being specific topics of interest.
- Understanding what type of distributions \(P_{XYZ}\) allow for the LOPC distillation of secret key.
- Computing new measures of secrecy for a given distribution and developing their operational meanings.
- Relating the problems of LOPC secrecy distillation and LOCC entanglement distillation.
- Generalizing to multi-party key distillation and relating to the structure of multipartite entanglement.
References
- Chitambar, E., Fortescue, B., and Hsieh, M.-H., “The Conditional Common Information in Classical and Quantum Secret Key Distillation.” IEEE Trans. Inf. Theory (2018); doi:10.1109/TIT.2018.2851564.
- Chitambar, E. and Hsieh, M.-H., “Round Complexity in the Local Transformations of Quantum and Classical States.” Nature Communications 8, 2086 (2017); doi:10.1038/s41467-017-01887-5.
- Chitambar, E., Fortescue, B., and Hsieh, M.-H., A Classical Analog to Entanglement Reversibility.” Phys. Rev. Lett. 115, 090501 (2015); doi:10.1103/PhysRevLett.115.090501.