Quantum information theory broadly studies the different ways to store, process, and communicate information based on the principles of quantum mechanics. The specific interests of this research group involve studying the mathematical theories and practical applications of quantum
entanglement and other fundamental quantum phenomena. A primary objective is to understand different ways that quantum-correlated systems can enhance distant communication and achieve information-theoretic security. This research applies tools and techniques from linear algebra, classical information theory and convex analysis.
Specific Research Topics
- Quantum Resource Theories:

A quantum resource theory is any model of restricted quantum information processing. The principles of quantum mechanics place certain limitations on what physical process are possible; for example the no-cloning theorem prohibits making copies of an unknown quantum source. However, in realistic scenarios, practical and non-fundamental constraints also limit what can be accomplished by a given quantum system. For instance, an experimentalist may only be able to maintain coherence in a quantum system for a short amount of time because of limited ability to mitigate environmental noise. Or, two separated quantum systems may only be able to communicate using classical signals since exchanging coherent quantum signals across macroscopic distances might be too resource-intensive. In these examples, certain features of a quantum system or quantum process become resources since they are beyond what the experimentalist can readily accomplish in the given context. A quantum resource theory pinpoints a particular quantum feature and provides an analytical framework for quantifying its resourcefulness and understanding its dynamical properties. The quantum resource theory framework is extremely broad, and it is used to characterize phenomena such as entanglement, faithful quantum communication, asymmetry, athermality, coherence, nonlocality, incompatibility, and more.
- Distributed Quantum Information Processing:
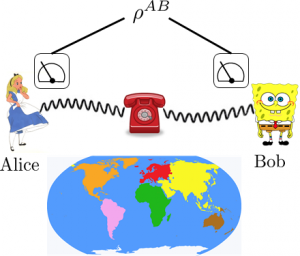
A general quantum system will consist of many different subsystems that are entangled and interacting with one another. These subsystems can be distributed to spatially separated quantum laboratories, thereby forming a quantum network. One scenario of both practical and fundamental importance arises when the individual quantum laboratories are unable to exchange subsequent quantum information with each other. Instead, they can act on their initially shared entangled states only by locally probing their respective subsystems and communicating with each other through the exchange of classical messages. This operational paradigm is called local operations and classical communication (LOCC), and it provides the basic framework for studying distributed quantum information processing. The simplest LOCC scenario involves two parties, generically called Alice and Bob, who initially share a two-part quantum system in state \(\rho^{AB}\). Alice can perform a sequence of measurements on her half and Bob can do likewise on his half. To coordinate their measurement strategy, Alice and Bob communicate classically over a telephone. In such a scenario, Alice and Bob cannot distribute entanglement to each other, but they must make use of their initial entanglement contained in \(\rho^{AB}\).
- “Quantum-Inspired” Information-Theoretic Security:
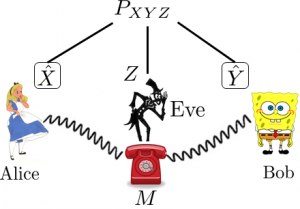
Information theory provides the tools to rigorously define the notion of security. A scenario that arises in certain cryptographic applications, such as quantum key distribution (QKD), involves two trustworthy parties (called Alice and Bob), along with an unwanted eavesdropper (called Eve). Each party has access to some (classical) system whose state is described by the random variable \(X\), \(Y\), and \(Z\), respectively. All these variables are correlated according to some joint probability distribution \(P_{XYZ}\). Alice and Bob’s goal is to utilize their shared correlations for private communication. Doing so involves processing their variables such that Eve’s overall correlation becomes decreased. Public communication between Alice and Bob can help in this task, and the operational framework is known as Local Operations and Public Communication (LOPC). LOPC is a classical cryptographic analog of LOCC in the quantum setting. Whereas quantum entanglement is the fundamental resource in LOCC processing, classical secrecy is the fundamental resource in LOPC processing.